连年来， 由于摩尔定律[1]的逐渐失效， 晶体管规模膨胀的本钱正以指数级的花样变得愈加不菲[2]， 从前主要依赖晶体管的规模扩大来升迁硬件性能的步调也逐渐变得难以终了. 为了赓续提高规范性能， 新的体紧缚构假想起初向特定领域架构(DSA)标的发展[3]. 这种转换也导致了现时超大规模集成电路假想(VLSI)的历程发生了报复的变化， 独特是对于专用硬件加快器的假想. 为了终了高效快速的硬件加快器假想， 采用高眉目空洞(HLS)算作基于初级硬件描绘言语(举例 Verilog 或 VHDL)的传统 VLSI 假想的替代有筹商[2色五月第二季，4]起初逐渐取得关注.
高眉目空洞(high-level synthesis， HLS)是一种将高等言语描绘的逻辑结构自动编削成硬件描绘言语抒发的电路模子的技能. 传统的HLS过程主要分为3个基本设施: 调治， 分拨与绑定[5]. 其中调治过程将规范中的每个操作分拨给特定的时钟周期， 并生成有限状态机， 以确保操作的法例和时代骄慢谋略需求. 分拨过程细目可供使用的硬件资源数量， 包括处理器单元， 存储器等， 并为每个操作分拨稳妥的资源. 绑定过程则通过在操作之间分享功能单元以及在变量之间分享寄存器或存储器来节俭面积， 从而终了资源的高效利用. 在给定的谋略任务和硬件资源拘谨下， HLS通过将谋略任务映射到可用的硬件资源上， 以终了最优的性能和资源利用率[6，7].
本文主要研究寄存器资源绑定问题， 即如何将规范的输入， 输出和临时变量映射到可用的寄存器单元上， 以最小化所需寄存器资源的问题. Brisk等东谈主[8]确认注解了静态单赋值(SSA)模样的规范的寄存器绑定问题不错在多项式时代内谋略出最优解. 学术界的进一步研究使命不错分为两个不同的标的: (1) 通过与电路假想历程中的其他问题协同研究， 寻找电路假想的全局最优解. 典型的如Rim等东谈主[9]将布图策动问题纳入绑定问题中进行协同筹商， 从而探索全局最优的布局与绑定有筹商. (2) 在寄存器绑定问题中引入位宽考量， 由于Brisk等东谈主[8]的研究限制了寄存器的大小必须富裕一致， 而在电子假想领域， 寄存器不错具有不同的长度. 通过放弃电路中的冗余位宽， 不错缩小电路的资源消耗， 这为进一步优化寄存器绑定问题提供了潜在的契机和可能性. 如Kum等东谈主[10]， Cong等东谈主[11]在传统图着色算法与团辩认算法[12]中加入位宽聘任计谋， 终了位宽感知的寄存器绑定算法研究， Canesche等东谈主[13]通过插入额外的复制和交换指示进行数据交换， 以减少寄存器资源的支拨.
寄存器绑定问题和寄存器分拨问题存在着诸多的相似性， 两个问题的中枢念念路都是依据变量的活跃信息终了寄存器分享， 这也启发现存的步调[11]将寄存器分拨的图着色抽象引入到责罚寄存器绑定当中. 然则两个问题存在着一个理会的各异: 寄存器分拨的目的是在寄存器数量固定的前提下将变量映射到寄存器中， 而寄存器绑定章需要生成所需的寄存器和连线. 这种各异性使得径直将寄存器分拨的图着色抽象应用于寄存器绑定问题时可能会激发多种问题. 领先， 寄存器分拨问题的抽象会给寄存器绑定问题引入无须要的拘谨限制， 如Cong等东谈主[11]将寄存器绑定问题映射为加权区间图着色问题(weighted-interval-graph coloring， WIGC)进行求解， 在此过程中需要对变量进行对王人限制， 这增加了变量的位宽和活跃区间， 从而导致了寄存器空间的浪费; 其次， 寄存器分拨中的一些优化手段并不适用于电路假想， 如Canesche等东谈主[13]的算法在寄存器绑定过程中引入了寄存器分拨中常见的活跃区间分割手段， 关联词， 在硬件中常常地移动数据会增加电路限定逻辑的复杂度， 反而可能会增加空洞后电路的面积.
针对上述问题， 本文冷漠一种针对寄存器绑定问题的多重图着色抽象. 由于HLS不错证据绑定生成所需的寄存器与对应连线， 无需辩认为寄存器组， 因此不需要解任对王人等寄存器分拨问题中常见的拘谨. 针对这些特色， 咱们将寄存器绑定问题映射为贯串多重着色(consecutive multi-coloring， CMC)问题， 对变量的位宽和活跃区间进行细粒度建模. 在此基础上， 咱们衡量了权重与极点的度的双重影响， 冷漠一种基于优先度的启发式算法， 该算法无需插入额外的复制与交换指示来进行数据交换， 并粗略进一步减少寄存器数量. 本文的主要孝敬包含以下3个方面.
• 咱们将寄存器绑定问题映射为贯串多重着色问题， 并冷漠一种在多项式时代内谋略表面下界的步调. 与传统步调中将该问题映射为加权区间图着色问题不同[11]， 咱们的步调无需引入额外的对王人拘谨， 更准确地建模了寄存器绑定问题中的变量位宽和活跃区间信息， 从而不错终了更节俭寄存器资源的分拨有筹商.
• 为了求解贯串多重着色问题， 咱们冷漠一种基于极点的度与权重感知的图着色算法(CMC-h算法). 具体而言， 算法领先使用CMC问题表面下界对应的分拨有筹商算作起初有筹商. 然后， 通过筹商极点的联贯联系和变量的位宽， 谋略每个极点的优先度. 终末， 按照优先度的法例进行求解， 以终了高效的寄存器绑定.
• 咱们在LLVM编译器[14]中终明晰上述算法， 并在MiBench[15]与Rosetta[16]测试集上对算法进行了实验评估. 评估抛弃标明， 在MiBench测试聚会CMC-h算法的绑定抛弃接近表面最优解， 在96.72%的样例中CMC-h的绑定有筹商是最优的， 比较于Cong算法[11]和Swap算法[13]分别将这一比例提高了31.5%和25.1%; 在Rosetta测试聚会， CMC-h的绑定有筹商在通盘测试样例中均阐明为最优解， 而Swap算法和Cong算法仅在93.10%和93.12%的样例中达到最优解.
1 筹商使命本节旨在详备先容与寄存器绑定问题筹商的研究使命. 寄存器绑定是高眉目空洞过程中一项基础优化问题， 其也可视为寄存器分拨问题的一种变体. 领先， 咱们将先容高眉目空洞过程中筹商的优化步谐和常用器具. 随后， 咱们将探讨寄存器绑定问题与寄存器分拨问题以及寄存器打包问题之间的相似性和各异性， 并评估各式算法在责罚这些问题时的适用性. 终末， 咱们还将询查位宽分析在寄存器绑定问题中的报复影响.
1.1 高眉目空洞高眉目空洞(HLS)是一种将高等言语描绘的逻辑结构自动编削成硬件描绘言语抒发的电路模子的过程. 该技能还是成为一种要害的使能技能， 尤其对于FPGA假想而言. 通过HLS， 假想者不错在软件层面上描绘组件的功能， 并自动生成相应的硬件代码， 从而终了软硬件责罚有筹商的快速部署. 相较于传统的电路假想步调， HLS使得假想者无须了解电路假想的细节， 从而不错将防御力更多地专注于算法逻辑结构的假想与假想空间的探索上. 已有的研究标明， HLS不错提高FPGA假想的开发遵守和可宝贵性[2，4，17].
传统的HLS过程主要分为3个基本设施: 调治， 分拨与绑定[5]. 其平分拨过程细目可供使用的硬件资源量， 调治过程将规范中的每个操作分拨给特定的时钟周期， 并生成有限状态机. 绑定过程通过在操作之间分享功能单元以及在变量之间分享寄存器或存储器来节俭面积. HLS在给定的谋略任务和硬件资源拘谨下， 将谋略任务映射到可用的硬件资源上， 以终了最优的性能和资源利用率. 这3个过程互相影响， 证据责罚它们的法例， 每个问题都有不同的责罚有筹商. 其中绑定问题平日是在分拨和调治之后制定和责罚的[6，7].
现在， HLS 器具还是在某些情况下粗略生成与手工优化电路相忘形的电路质地[2]. 经过多年的发展， 还是阐明出高出30种不同的HLS器具[18]， 其中多个器具基于开源编译器框架LLVM/GCC等进行开发. 举例， 多伦多大学研发的LegUp[19]利用 LLVM 编译器算作前端编译器， 粗略将输入的C言语自动编削为适用于 FPGA 的 Verilog 言语. 另一个开源器具 Bambu[6]也采用 LLVM/GCC的规范IR算作输入， 终明晰庸碌的编削和优化范围， 为EDA领域的研究东谈主员提供了探索和集成新步调的契机.
1.2 寄存器绑定问题关联问题寄存器绑定问题平日被拿来与寄存器分拨问题和寄存器打包问题互比较较. 寄存器绑定对电路中的寄存器资源进行分享， 提高资源的利用率. 寄存器分拨细目如何将规范中的变量分拨给有限数量的寄存器， 以最小化内存探询次数并提高实行遵守. 而寄存器打包则波及如何将变量组合在一王人， 并分拨给不同的寄存器取悦， 以最猛进度地利用寄存器容量. 天然这些问题在具体细节上存在各异， 但它们都波及优化寄存器的使用， 因此在责罚某个特定问题时， 不错鉴戒其他关联问题的步调进行求解.
寄存器分拨问题平日被合计是一个NP富裕问题， 因此在试验应用中常采用图着色算法进行求解[20]. 关联词， 在2005–2006年间， 基于静态单赋值(SSA)模样的规范， 寄存器分拨问题被确认注解不错在多项式时代内取得最优解[21−23]. 寄存器绑定问题与寄存器分拨的主要区别在于: 寄存器绑定问题中的寄存器大小是任性长度， 相较于平日的架构， 对寄存器的探询愈加天真[24]. 因此， 若采用传统的寄存器分拨算法来责罚寄存器绑定问题， 则会引入过多传统架构的限制， 导致绑定的抛弃较差.
寄存器打包问题试图通过变量合并的花样[25]将多个变量分拨到吞并寄存器的不同位中， 从而责罚可变位宽的寄存器分拨问题[26−28]. 该问题限制了寄存器组的大小为固定的大小. 尽管与寄存器绑定问题存在一定的相似性， 但在传统硬件假想领域中， 将多个变量分拨到吞并寄存器的不同位中会导致物理寄存器布局变得极为复杂， 同期也会增加物理寄存器的寻址和存储蔓延. 因此， 这种技能恒久受到一定进度的限制[28]. 当将寄存器打包算法应用于寄存器绑定问题时， 试验的分拨后果可能稍逊于Cong等东谈主冷漠的步调[11，27].
1.3 位宽分析位宽分析算作位宽感知的寄存器绑定算法的基本组成部分， 主要利用静态分析技能推断变量的位宽[29−31]. 传统高等言语如C/C++等描绘电路的逻辑结构存在很大局限性， 因为这些言语只提供具有受限长度的谋略类型， 举例固定位宽的8/16/32/64等. 研究炫夸， 在一组用C编写的基准规范中， 平均有40%的位宽冗余[29]， 识别出这些过剩的比特不错缩小潜在的硬件资源本钱. 申饬公式[32−34]标明， 乘法器的面积与两个输入的位宽乘积成正比， 加法器的面积则与输入的位宽成正比. 对于寄存器和多路复用器等其他资源类型， 不错采用合理的线性假设来揣度它们的面积和位宽之间的联系. 由于操作位的减少也不错带来布线本钱的节俭， 因此通过优化电路的位宽分拨， 还不错灵验地减少电路的面积和功耗. 关联词， 从传统物理瞻仰限制动身为硬件假想明确指定比特宽度费时劳作. 因此更祈望的假想历程是自动分析变量和操作的位宽， 以削弱假想者的包袱并减少出错的契机. 本文的寄存器绑定算法未限制位宽分析的具体终了花样， 因此， 任何终了花样都不错骄慢咱们的需求.
现时编译器主要从范围分析与位掩码分析两种层濒临变量位宽进行分析. Stephenson等东谈主[29]冷漠了基于变量范围分析的位宽分析技能， 该步调试图通过变量范围的正向与反向传播来揣度变量的范围， 从而终了对变量的高位截断技能. Gort等东谈主[35]冷漠了掩码分析与范围分析相结合的位宽分析技能， 使得位宽分析不错针对变量的每个比特进行精准的分析. 这两种分析模样提供了不同层面的互补信息， 因此需要空洞筹商[35].
2 布景常识与研究动机本节主要对筹商布景常识与研究动机进行梳理， 领先咱们对后文将要波及的图论筹商常识进行通俗先容. 然后咱们给出本文所关切的寄存器绑定问题的界说与典型样例. 咱们领先先容一种寄存器绑定问题的经典抽象步调加权区间图着色(WIGC)抽象[11]. 接着咱们先容一种通过插入额外的拷贝指示在多项式时代内给出最优解的优化算法[13]. 终末咱们通过样例分析指出了两种步调中存在的寄存器浪费征象， 并由此引出咱们新的假想.
2.1 布景常识本节回想了弦图表面中的筹商想法. 对于无向图$ G(V， E) $， 图上的一个环中不相邻的两个极点相连的边称为弦. 给定无向图$ G(V， E) $， 要是图中任何一个长度大于3的环至少有一条弦， 则称$ G $是弦图.
咱们使用$ N(v) $表现与极点$v$相邻的极点取悦， 若一个图的子图极点两两相邻， 则称该子图为团， 咱们记极点数最多的团为最大团， 其极点数记为团数$ \omega (G) $. 要是极点$ v \in V $的邻域$ N(V) \cup \left\{ v \right\} $是一个团， 则称该点为单纯点. 咱们称一个点的序列$ {v_1}， {v_2}， \ldots ， {v_n} $为一个完好放弃序列(PEO)， 当且仅当该序列骄慢极点$ {v_i} $在$ {v_i}， {v_{i + 1}}， \ldots ， {v_n} $的教唆子图中为一个单纯点.
给定一些区间， 用每个极点表现一个区间， 若两个区间的错杂非空， 则代表两区间的极点间存在一条边， 由此组成的图称为区间图. 对于弦图与区间图， 有如下几个报复的论断[23].
定理 1. 无向图$ G(V， E) $是弦图当且仅当$ G $存在完好放弃序列.
定理 2. 弦图$ G $的色数$ \chi (G) $等于团数$ \omega (G) $.
引理 1. 区间图必定为弦图.
引理 2. 弦图$ G $按照PEO逆序蓄意着色， 该有筹商的着色数等于$ \chi (G) $.
引理 3. 区间图按极点对应区间的右端点从小到大排序， 该序列为完好放弃序列.
2.2 寄存器绑定问题界说由于本文关注的问题是调治后的寄存器绑定问题， 因此如无额外确认， 假设后文说起的每个输入规范都是骄慢SSA模样的线性结构规范， 且本文中的寄存器绑定问题不波及指示间的调治. 以下给出寄存器绑定问题界说.
界说1. 寄存器绑定问题. 给定规范$ P $的变量取悦$ V $， 独特权重映射$ w:V \to \mathbb{N} $， 假设每个变量$ v \in V $都存在对应活跃区间$ {l_v} $， 映射$ I $为每个变量$ v \in V $分拨一个区间$ I(v) $， 且骄慢如下拘谨:
a) (区间拘谨) $\forall v \in V，\; \left| {I(v)} \right| = w(v)$.
b) (冲突联系) $ \forall a， b \in V $， 若$ {l_a} \cap {l_b} \ne \varnothing $， 则$ I(a) \cap I(b) = \varnothing $，
其中， $ \mathbb{N} $代表天然数集， 权重映射$ w $代表每个变量的位宽. 该界说与Cong等东谈主冷漠的绑定问题界说[11]是一致的， 但这里强调了绑定有筹商$ I $会单独筹商变量的每个比特分拨情况. 与传统的寄存器分拨问题将每个寄存器视为固定的位宽不同， 寄存器绑定问题允许证据变量的位宽天真地诊治寄存器的位宽. 这种天真性有助于减少所需的寄存器数量， 从而最猛进度地利用寄存器资源.
例1: 图1左侧是一段通俗的规范源码示例， 在该样例中咱们忽略调治等其他HLS过程， 图1右侧对该示例的寄存器绑定问题进行了愈加详备的展示[13]. 图的横向每个方框表现1比特位， 举例变量$ a $需要至少5位的寄存器; 图的纵向的每条横线记号了不同的规范点， 用于表现变量的活跃区间. 每个变量的位宽与活跃区间组成了一个矩形， 因此， 不错简化地说寄存器绑定问题的责罚有筹商应尽可能密致地打包通盘的矩形， 而不允许重复.
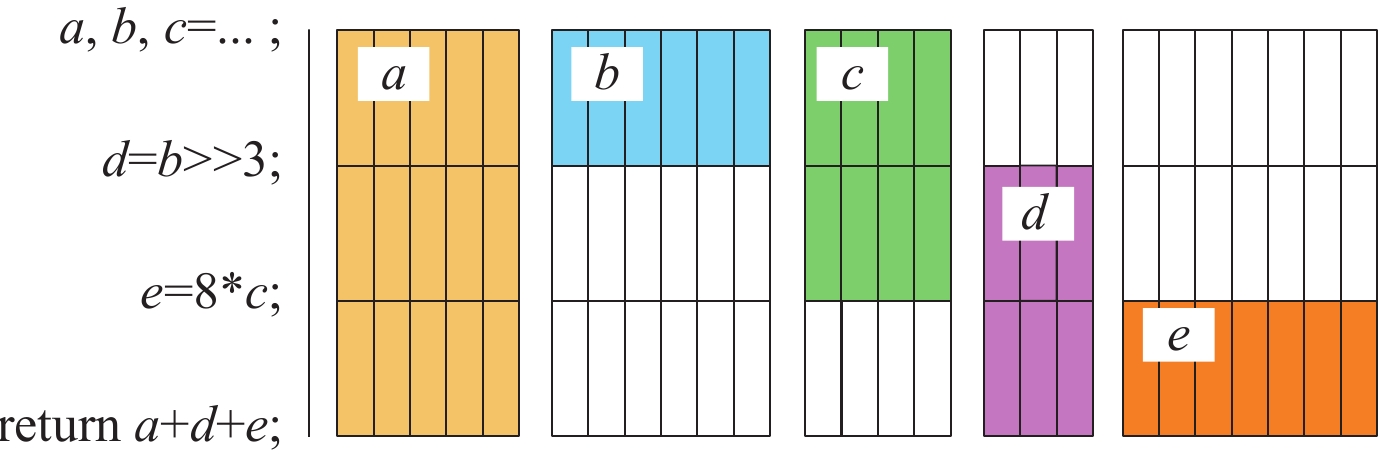图 1 样例例源码与变量位宽-活跃区间表现图
2.3 加权区间图着色抽象
Cong等东谈主[11]将寄存器绑定问题转换为加权区间图着色问题进行求解， 从而允许寄存器以任性位宽进行绑定， 咱们领先给出其基本界说.
对于给定规范$ P $， 不错导出区间图$ G(V， E) $. 其中每个极点$ v \in V $对应于规范中的变量， 边$ (a， b) \in E $， 当且仅当两个极点$ a， b \in V $对应变量的人命周期互相重复， 即它们弗成绑定到吞并个寄存器中. 给图$ G $的每个极点$ v $赋予一个权重$ w(v) $表现对应变量的位宽， 咱们称该图为加权图， 并记为$ G(V， E， W) $. 落寞集是指图中互不相邻的极点组成的取悦. 假设$C = \left\{ {{c_1}， {c_2}， \ldots ， {c_k}} \right\}$是图$ G(V， E) $的某一着色有筹商， 该有筹商将极点取悦$ V $辩认为$ k $个落寞集$ {V_1}， {V_2}， \ldots ， {V_k} $， 其中$V_i$表现第$ i $个落寞集， $ {c_i} $表现$ {V_i} $中的变量所着的心理. 若界说落寞集$ S $的权重为$ w(s) = \max \left\{ {w(v)|v \in S} \right\} $， 心理$ {c_i} $的权重界说为$ w({V_i}) $， 则着色有筹商$ C $的权重不错界说为:
$ \Phi (G， C) = \sum\nolimits_{i = 1}^k {w({V_i})}. $基于以上界说， 位宽感知的寄存器分拨问题不错映射为加权区间图着色问题， 界说如下.
界说2. 加权区间图着色问题. 给定加权区间图$ G(V， E， W) $， 求解使得权重函数$ \Phi (G， C) $最小化的着色有筹商$ C $.
WIGC问题在某些研究使命中也被称为区间图的最大着色问题(max-coloring problem)[36]. 当极点的权重一致时， 这个问题不错在多项式时代内责罚， 关联词对一般问题而言， 该问题已被确认注解是NPC问题[36，37]. WIGC问题的表面下界不错通过子图的色数进行揣度. 咱们将图$ G $按照极点的权重辩认子图， 并按权重从大到小排序为${G_1}， {G_2}， \ldots ， {G_m}$， 子图$ {G_i} $的极点对应的权重记为$ {w_i} $， 记$ {U_i} = \bigcup\nolimits_{j = 1}^i {{G_j}} $， $ {k_i} = \chi ({U_i}) - \chi ({U_{i - 1}}) $， $ {k_1} = \chi ({G_1}) $. 则WIGC下界不错通过如下公式进行揣度:
$ L(G) = \sum\nolimits_{i = 1}^m {{w_i} \cdot {k_i}}. $Cong等东谈主[11]冷漠了一种基于WIGC抽象的启发式算法， 咱们称之为Cong算法. 该算法领先将变量按位宽降序成列， 通过启发式步调将位宽邻近的变量合并装入吞并个寄存器中进行分拨. 图2(b)炫夸了Cong算法对例1的责罚有筹商. 在该有筹商中， 变量$ b $和变量$ e $分享一个7位寄存器， 而其余变量则分别使用与它们的位宽疏通的寄存器， 悉数需要分拨19位寄存器.
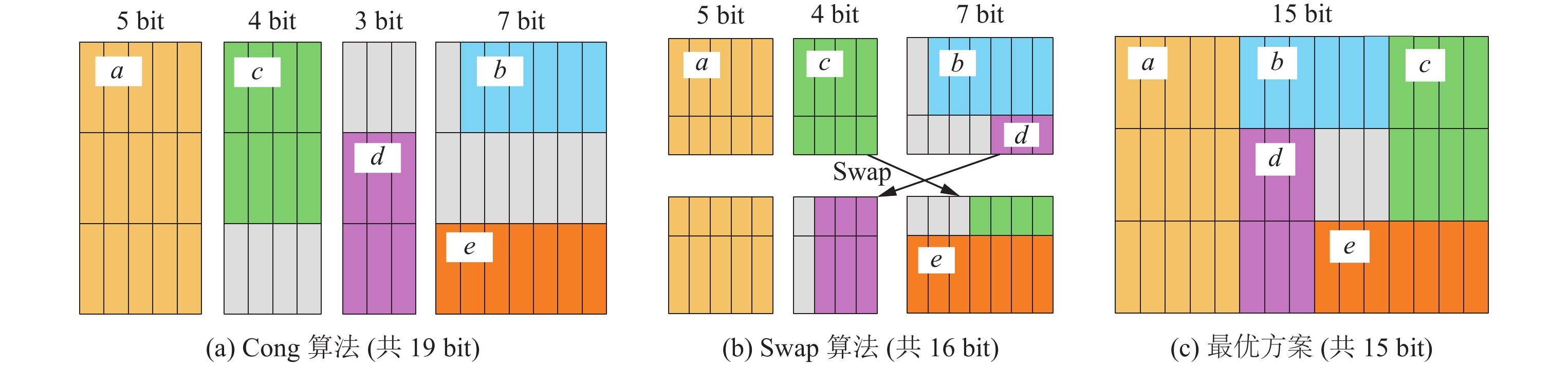图 2 3种寄存器绑定有筹商对例1产生的分拨抛弃表现图
2.4 Swap算法
Canesche等东谈主[13]在WIGC抽象的基础上， 进一步冷漠了通过插入复制和交换指示来缩小寄存器数量的步调， 咱们称之为Swap算法.
Swap算法领先在每个基本块中的贯串指示之间插入并行拷贝， 从而将每个变量的活跃区间限制在了相邻的两条指示之间， 不同规范点间的活跃变量互相落寞. 接着独随即责罚每个规范点上的加权区间图着色问题. 终末， Swap算法尝试合并多个规范点不同着色有筹商， 并给出的最优拼接有筹商. Swap算法对例1的责罚有筹商需要在第2和第3条指示之间插入交换指示， 以便将变量$ c $和$ d $的活跃区间分割开来. 这么， 变量$ c $和$ d $的部分活跃区间不错与变量$ b $和$ e $分享一个7位寄存器， 而其余活跃区间不错分享一个4位寄存器. 该有筹商悉数需要分拨16个寄存器. 与Cong算法步调比较在比特位宽上共减少了3位， 但同期需要增加一条交换指示.
Swap算法以插入额外指示为代价减少了绑定的寄存器数量， 它是WIGC抽象的一种改良模样， 由于过程中的每一步算法均是最优解， 因此Swap算法是一种多项式时代的最优解算法. 但Swap算法的最优性限制在该算法缔造的对王人拘谨之中， 对于通盘寄存器绑定问题的求解并非最优， 咱们将在第2.5节中详备确认.
2.5 研究动机本节通过样例分析仔细研究了Cong算法与Swap算法可能形成的寄存器浪费征象， 并由此指出已有算法的局限性. 咱们将在第3节中通过引入新的抽象来责罚这些问题.
为了使接下来的分析愈加透露明确， 咱们将绑定算法中寄存器的安静状态界说为寄存器空泡， 并通过对寄存器空泡的分析来评估已有算法的分拨有筹商. 一般而言主要寄存器空泡包括两种不同的状态， 一是变量位宽与寄存器大小不匹配产生的位宽冗余， 二是由于冲突联系形成的寄存器空置. 图2中的灰色区域展示了不同绑定有筹商产生的寄存器空泡， 平日咱们合计寄存器空泡的范围越大， 形成寄存器浪费的可能性也就越高.
Cong算法将可能同期产生两种类型的寄存器空泡. 如图2(a)所示， 变量$ b $与变量$ e $合并时， 6 bit变量$ b $存储在7 bit寄存器中， 产生了1 bit的位宽冗余; 变量$ b $的活跃区间抛弃， $ e $的活跃区间起初之前， 寄存器处于安静状态且无法被其他变量复用， 从而产生了寄存器空置. 因此Cong算法在3种绑定有筹商中产生了最多的寄存器空泡.
Swap算法通过插入交换与并行拷贝指示， 责罚了寄存器空置产生的寄存器空泡问题， 但却仍然存在两点劣势. 其一， Swap算法需要合并多个子着色有筹商， 在合并过程中会扩大合并的寄存器大小， 因此增加了位宽冗余产生的寄存器空泡. 如图2(b)所示的4 bit寄存器， 是由子着色有筹商的4 bit寄存器与3 bit寄存器合并而成， 因此形成了额外的位宽冗余. 其二， 拷贝指示产生额外代价. Swap算法常常地移动数据会使得电路的限定逻辑变得更为复杂. 如图2(b)所示， 算法插入了额外的交换指示， 这可能会增增加路复用器的使用， 反而导致空洞后的电路面积更大， 咱们将在第4.5节详备确认这一矛盾.
已有绑定算法产生大都寄存器空泡的根底原因在于对寄存器的利用存在不对理的限制. 与寄存器分拨问题不同， 寄存器绑定问题中， 寄存器的连线不错证据绑定抛弃生成， 无需解任通用可编程寄存器常见的对王人拘谨. Cong算法采用的WIGC抽象， 仅允许吞并落寞集内的变量分享吞并个寄存器， 为寄存器绑定问题引入了额外的对王人拘谨. Swap算法天然对WIGC抽象有所改良， 但仍未粗略富裕放弃对王人拘谨带来的影响. 如图2(c)所示炫夸了一种最优的绑定有筹商， 该有筹商将寄存器空间视为一个贯串的线性空间， 任何探询都通过一段区间来表现， 不同的变量分享吞并个寄存器的不同比特位. 在该分拨有筹商中， 变量$b， \;c， \;d，\; e$错位地分享了一部分寄存器， 共需15位寄存器， 比较于Swap算法进一步减少了1位寄存器， 且无需插入额外的指示. 这是WIGC抽象步调所无法终了的寄存器绑定有筹商. 因此咱们需要冷漠一种新的抽象， 该抽象粗略愈加解放地描绘变量之间的分享联系， 且不会产生额外的寄存器拘谨.
3 图的贯串多重着色抽象在本节中， 为了责罚已有算法中存在的问题， 咱们引入了图的贯串多重着色模子. 领先， 咱们给出了贯串多重着色问题的明确界说. 接下来， 咱们对贯串多重着色问题的表面下界进行了详备分析， 以算作评估和假想咱们算法的依据. 终末， 为了试验责罚寄存器绑定问题， 咱们冷漠了一种基于优先度的启发式算法， 该算法不需要插入额外的拷贝指示， 且比较于已有算法粗略进一步减少寄存器的数量.
3.1 贯串多重着色抽象证据第2.5节的分析抛弃， 咱们冷漠一种图的贯串多重着色抽象来对寄存器绑定问题进行求解. 为了更透露地确认咱们的念念路色五月第二季， 咱们领先引入图的多重着色问题(multi-coloring， MC)的界说.
界说3. 图的多重着色问题. 给定加权图$ G(V， E， W) $， 对每个极点$ v \in V $染$ w(v) $种不齐心理， 记心理取悦为$ C(v) $， 求解相宜条目的着色有筹商， 使得对于任性边$ (a， b) \in E $， 都有$ C(a) \cap C(b) = \varnothing $配置.
咱们记MC问题的最小色数为$ \gamma (G) $. MC问题强调了咱们对于寄存器绑定问题中变量之间更为天确凿分享花样的建模， 它不错很好地描绘比特粒度的寄存器分享问题. 在MC问题中， 每个极点$ v $的心理取悦$ C(v) $不错视为按比特粒度分拨的寄存器， 而每个边$ (a， b) $则不错视为两个变量$ a， b $的探询冲突. 然则， MC问题并弗成试验地责罚寄存器绑定问题， 因为该问题中的心理取悦$ C(v) $是翻脸的， 而寄存器的探询则是贯串的， 无法骄慢寄存器绑定问题中的区间拘谨.
为了试验地责罚寄存器绑定问题， 咱们进一步界说心理集的贯串性. 咱们称心理取悦$ C(v) $是贯串的， 当且仅当存在某个$ k \in \mathbb{N} $， 使得$ |C(v) \cap [k， k + w(v))| = w(v) $. 在此基础上， 咱们冷漠了图的贯串多重着色问题， 其界说如下.
界说4. 图的贯串多重着色问题. 给定加权图$ G(V， E， W) $， 求解骄慢条目的多重着色有筹商， 使得任性极点$ v \in V $的心理取悦$ C(v) $是贯串的.
贯串多重着色问题在某些研究使命中也被称为区间着色(interval coloring)问题[37]. 该问题与寄存器绑定问题是等价的， 因为寄存器绑定问题中的规范$ P $不错逐一映射为CMC问题中的加权图$ G(V， E， W) $， 其中变量取悦映射为图的极点取悦， 变量的位宽映射为极点权重， 变量的冲突联系映射为图的边， 寄存器取悦映射为心理取悦， 区间拘谨则映射为心理取悦的贯串拘谨. 咱们记CMC问题的最小色数为$ {\gamma ^*}(G) $.
CMC抽象精准描绘了每个变量分拨在寄存器中的位宽与活跃区间， 无需解任额外的对王人拘谨. 对于任性一个WIGC问题的解$ C $， 老是不错通过将$ C $中的每个寄存器拼接成为一个大寄存器得到一个CMC问题的解， 反之CMC问题的解却不一定是WIGC问题的解. 因此CMC抽象比较于WIGC抽象愈加契合寄存器绑定问题， 粗略愈加天真地描绘变量之间的复用联系.
图2(c)炫夸了CMC抽象的一种多重着色有筹商. 在该着色有筹商中， 变量$ a $被分拨到了寄存器$R[14{\text{:}}10]$， 变量$ b $被分拨到了寄存器$R[9{\text{:}}4]$， 变量$ c $被分拨到了寄存器$R[3{\text{:}}0]$， 变量$ d $被分拨到了寄存器$R[9{\text{:}}7]$， 变量$ e $被分拨到了寄存器$R[6{\text{:}}0]$. 该着色有筹商的色数为15， 而WIGC抽象对该样例抛弃的表面下界范围为$ L(G) = 16 $， 因此CMC抽象破裂了WIGC抽象抛弃的表面下界.
3.2 表面下界分析即使对于区间图， CMC问题仍然已被确认注解是NPC问题[36，37]， 因此咱们无法在多项式时代内给出该问题的解. 但算作参考， 在咱们不错在多项式时代内给出该问题的表面下界.
由于CMC问题是MC问题的特例， $ \gamma (G) \leqslant {\gamma ^*}(G) $， 因此， MC问题的最优解即为CMC问题的表面下界. 对于SSA模样的线性结构规范$ P $， 其对应的干预图为区间图， 对于区间图咱们不错有更多锻真金不怕火的论断.
引理 4. 区间图的MC问题多项式时代可解.
确认注解: MC问题不错转换为图着色问题进行求解， 只需将每个极点转换为对应色数的富裕子图， 从而编削为传统图着色问题进行求解. 证据引理 1， 区间图必定是弦图， 编削后映射到对应图着色问题中也必定为弦图. 因此区间图的MC问题不错转换为弦图的图着色问题. 证据定理 2， 该问题必定在多项式时代内可解. 因此， 区间图的MC问题也不错在多项式时代内求解.
咱们给出无需构建干预图的表面下界算法， 如算法1所示， 算法在第2行按照变量活跃区间的终端从大到小排序， 按照引理 3， 该法必然定为对应区间图的完好放弃序列的逆序. 咱们在第5行对变量的每个比特进行编号， 从而将对应加权区间图转换为区间图， 对区间图的每个极点分别进行着色， 其中每个极点对应变量的每个比特. 算法第8–21行按照完好放弃序列逆序对区间图的每个极点进行着色. 其中第13–15行利用了完好放弃序列的性质， 在无需构建干预图的情况下仍然粗略宝贵每个极点$ v $的邻居节点$ N(v) $的已着色情况. 该算法的时代复杂度为${\rm{O}}(\left| V \right| + \left| E \right|)$， 其中排序算法的时代复杂度平日为${\rm{O}}(\left| V \right|\log \left| V \right|)$， 但在该问题中， 不错利用桶排序算法加快到${\rm{O}}(\left| V \right|)$[23].
算法1. 表面下界分析.
Input: 变量列表$ V $， 每个变量$ v \in V $的位宽$ {W_v} $与活跃区间$ {I_v} $;
Output: 表面下界$ L $.
1. function $ LowerBound(V， W， I) $
2. ${\mathit{Sort}}(V， key \leftarrow lambda$$\left.v: I_{v} {.end， reversed } \leftarrow {\rm{True}}\right)$
3. $ M \leftarrow 0 $
4. for$ v \in V $do
5. $ inde{x_v} \leftarrow [M， M + {W_v}) \cap \mathbb{N} $
6. $ M \leftarrow M + {W_v} $
7. end for
8. $freeColo{r_i} \leftarrow {\rm{True}}， \forall i \in [0， M) \cap \mathbb{N}$
9. $ Colo{r_v} \leftarrow \varnothing ， \forall v \in V $
10. $ lastEnd \leftarrow {I_{{V_0}}}.end $
11. $ kil{l_i} \leftarrow \varnothing ， \forall i \in [0， lastEnd) \cap \mathbb{N} $
12. for$ v \in V $do
13. $ kil{l_{{I_v}.start}} \leftarrow kil{l_{{I_v}.start}} \cup \left\{ v \right\} $
14. $freeColo{r_{colo{r_i}}} \leftarrow {\rm{True}}， \forall i \in inde{x_u}， u \in kil{l_k}， k \in [{I_v}.end， lastEnd] \cap \mathbb{N}$
15. $ lastEnd \leftarrow {I_v}.end $
16. for$ i \in inde{x_v} $do
17. $j \leftarrow \min \left\{ {k|freeColo{r_k} = {\rm{True}}} \right\}$
18. $ Colo{r_v} \leftarrow Colo{r_v} \cup \left\{ v \right\} $
19. $freeColo{r_j} \leftarrow {\rm{False}}$
20. end for
21. end for
22. $ L \leftarrow \max (Color) $
23. return $ L， Color， index $
24. end function
图3(a)炫夸了例1规范对应的干预图， 图中的极点$ a， b， c， d， e $分别被平分为$ 5， 6， 4， 3， 7 $份， 代表每个极点不错着多种不同的心理. 图3(b)炫夸了按照完好放弃法例$ \left\{ {b， c， e， d， a} \right\} $的逆序着色的一种多重着色的最优分拨有筹商. 在该有筹商中， 变量$ b $被分拨给了翻脸的寄存器$ \left\{ {5， 6， 7， 12， 13， 14} \right\} $中， 不骄慢0的第2个拘谨， 即区间拘谨. 但若按照另一种完好放弃法例$ b， c， a， d， e $的逆序进行着色， 其着色有筹商就如图2(c)所示， 为一种贯串的多重着色有筹商.
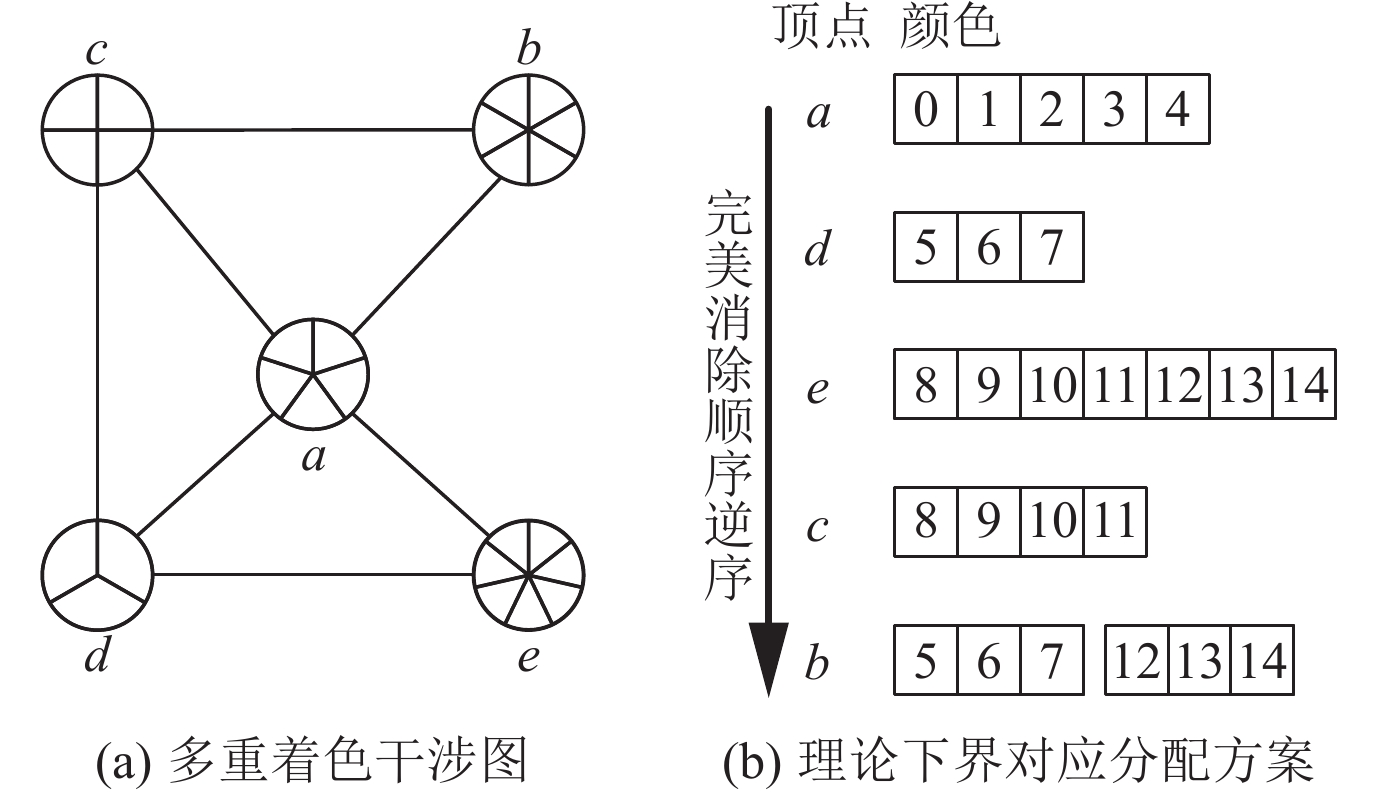图 3 图的多重着色干预图与分拨表现图
3.3 贯串多重着色算法
为超过到试验挑升念念的寄存器绑定有筹商， 咱们筹商径直对CMC问题进行求解. 由于咱们现在难以在多项式时代内求解CMC问题的最优解， 因此咱们冷漠了一种基于优先度的启发式步调， 称之为CMC-h算法(如图4). 它的基本念念想是按照优先度法例对极点进行蓄意着色， 其中优先度的假想对图着色问题中报复的分拨依据极点的度与CMC问题中极点专有的特征极点权重进行了空洞筹商. 咱们在第4节中实考确认注解了， 该算法的平衡筹商在试验求解中取得了优异的分拨后果.
图 4 CMC-h算法的一般历程
咱们领先界说加权图$ G(V， E， W) $的度， 对任性极点$v \in V $， 咱们界说极点的度为其邻居节点的权重和， 即$ d(v) = \displaystyle\sum\nolimits_{u \in N(v)} {w(u)} $， 其中$ N(v) $代表了极点$ v $的邻居节点取悦， 由此咱们界说极点的优先度为:
$ r(v) = \alpha {d^*}(v) + (1 - \alpha ){w^*}(v)， $其中， $ {d^*}(v)， {w^*}(v) $为归一化后极点的度与权重， $ \alpha \in [0， 1] $为参数.
咱们按照变量的优先度法例进行蓄意着色， 算法2展示了CMC-h算法的具体过程. 算法的第2行， 咱们领先对问题进行表面下界分析， 并得到起初的着色有筹商， 只须在该有筹商不贯串的情况下， 咱们才会采用启发式步调进行着色. 平日， 咱们聘任$ \alpha \in \{ 0， 0.5， 1\} $进行3次着色并聘任最优抛弃， 咱们将在第4.3节中进行详备陈诉. 算法的第6行， 咱们谋略了变量的优先度， 该优先度决定了极点着色的法例. 在这里咱们对极点的度与权重进行了归一化处理. 第8–16行代表了按照优先度法例进行贯串着色的过程. 与谋略表面下界时有所不同， 由于无法通过完好放弃序列快速谋略现时极点的已着色情况， 因此咱们在第4行构建了完整的干预图. 其中， 构建的干预图为加权图， 需要为每个极点赋予等于该极点对应变量位宽的权重. 在第11， 12行需要每次再行谋略极点 的邻居节点 的已着色情况. 第13， 14行要求对吞并极点染多种贯串的心理， 而不是每个比特分别着色， 从而保证每个极点的心理取悦均是贯串的.
着色算法的时代复杂度为${\rm{O}}(\left| V \right| + \left| E \right|)$， 排序算法的时代复杂度为${\rm{O}}(\left| V \right|\log \left| V \right|)$， 构建干预图的时代复杂度为${\rm{O}}({\left| V \right|^2})$， 因此算法的举座复杂度仍然为${\rm{O}}({\left| V \right|^2})$.
算法2. CMC-h算法.
Input: 变量列表$ V $， 每个变量$ v \in V $的位宽$ {W_v} $与活跃区间$ {I_v} $;
Output: 着色有筹商$ Color $.
1. function $ CMC - h(V， W， I) $
2. $ L， Color， index \leftarrow LowerBound(V， W， I) $
捆绑 调教3. if $ \neg isContinue(Color) $then
4. $G(V， E， W)\leftarrow {\mathit{BuildInterferenceGraph}}(V， W， I)$
5. for$ \alpha \in \{ 0， 0.5， 1\} $do
6. $ r(v) = \alpha {d^*}(v) + (1 - \alpha ){w^*}(v)， \forall v \in V $
7. ${\mathit{Sort}}(V， key \leftarrow lambda$$v:r(v)， reversed \leftarrow {\rm{True}})$
8. $ Colo{r_v} \leftarrow \varnothing ， \forall v \in V $
9. $ done \leftarrow \varnothing $
10. for$ v \in V $do
11. ${ freeColor }_{i} \leftarrow \text { True }， \forall i \in[0， M) \cap \mathbb{N}$
12. $freeColo{r_i} \leftarrow {\rm{False}}， \forall i \in {\mathit{index}}{_u}， u \in N(v) \cap done$
13. $j \leftarrow \min \left\{ {k|freeColo{r_s} = {\rm{True}}， \forall s \in [k， k + {W_v}) \cap \mathbb{N}} \right\}$
14. $ Colo{r_v} \leftarrow Colo{r_v} \cup ([j， j + {W_v}) \cap \mathbb{N}) $
15. $ done \leftarrow done \cup \left\{ v \right\} $
16. end for
17. if$ \max (Color) = L $then
18. return$ Color $
19. end if
20. end for
21. end if
22. return $ Color $
23. end function
4 实验评估 4.1 实验环境本节将从如下几个角度分别对本文冷漠的使命进行评估.
1) 本文冷漠的贯串多重着色抽象(CMC抽象)比较于第2节先容的Cong算法和Swap算法的区别是什么， 它们分别轨则了怎样的问题求解范围.
2) 本文冷漠的启发式算法(CMC-h算法)的试验分拨后果如何， 与Cong算法和Swap算法比较较后果如何.
3) CMC-h算法进行寄存器绑定需要多永劫间.
4) CMC-h算法谋略的绑定有筹商是否可空洞， 对逻辑空洞会形成怎样的影响.
本文寄存器绑定算法应用的单元是一个函数， HLS中调治与绑定平日被辩认为落寞的优化过程， 且寄存器绑定平日是在调治之后的资源绑定阶段进行， 因此调治算法的聘任并不影响本文寄存器绑定算法的灵验性. 为了模拟寄存器绑定的输入， 咱们按照尽早调治原则(ASAP)进行调治[1]， 然后再进行寄存器绑定算法的评估.
咱们在LLVM 11.0.0 版块中终明晰本文冷漠的技能， 使用LLVM自带的位宽分析功能处理前置的分析使命. 同期使用了MiBench[15]与Rosetta[16]套件算作测试集， 如表1所示， MiBench是一组共35个具有营业代表性的用于基准测试的镶嵌式应用规范， 波及工业自动化， 消费类开荒， 办公， 采集， 安全与通讯这6个不同的类别; Rosetta是一组针对真实场景的 FPGA 的基准测试套件， 包括机器学习与视频处理等热点场景下的多个富裕开发的应用规范. 实验在Intel Xeon Gold 6248 CPU 20核处理器上进行， 时钟为2.50 GHz. 使用的操作系统是Ubuntu Linux LTS 20.04版块. 咱们的终了将代码生成为LLVM机器代码中间表现(MIR)， 并使用LLVM中还是存在的寄存器分拨基础设施进行分拨. 咱们并莫得将这些抛弃映射到逻辑门中， 因为咱们短缺必要的器具来作念这件事. 关联词算作一个想法的考证， 咱们将一些分拨抛弃手动翻译成了Verilog并进行空洞分析， 咱们将在第4.5节进行具体的解释.
表 1 MiBench测试集[15]与Rosetta测试集[16]
咱们对MiBench[15]中的609个函数与Rosetta[16]中的22253个函数进行了分析与测试. 表2回想了寄存器绑定的汇总抛弃， 其中运行时代以毫秒为单元， 寄存器大小以位为单元， “Geo”是几何平均值， “Avg”是算术平均值. 抛弃炫夸在MiBench测试聚会CMC-h算法比较于Swap算法和Cong算法分别减少1.8%和1.4%的寄存器， 同期比较于最优解仅多使用0.13%的寄存器资源; 在Rosetta测试聚会CMC-h算法比较于Swap算法和Cong算法分别减少1.97%和1.98%的寄存器， 同期在通盘的测试用例中CMC-h算法均达到了最优解.
表 2 绑定测试抛弃对比汇总(以函数为单元)
4.2 CMC抽象的最优解评估
本节评估了CMC抽象的最优解比较已有步调的表面最优解的辞别， 进而标明咱们引入CMC抽象的必要性. 其中CMC问题的最优解通过对CMC-h算法未达到表面下界的样例分析， 采用整数线性策动步调(ILP)精准求解得到， 在给出的测试聚会咱们暂未发现试验的最优解不等于咱们给出的表面下界的样例， 但咱们仍无法在表面上确认注解$ \gamma (G) = {\gamma ^*}(G) $. Cong算法的最优解咱们现在无法准确求解， 但咱们不错通过第2.4节给出的表面下界$ L(G) $代替， 试验的最优解抛弃将不小于该值. 而Swap算法的分拨抛弃自己便是在其抽象问题下的一种表面最优解.
图5炫夸了MiBench测试聚会CMC抽象的最优解， Cong算法的表面下界与Swap算法的最优解之间的对比， Cong算法的表面下界与Swap算法的最优解分拨抛弃是一致的， 因此咱们在图5中合并展示. 其中， 横轴上的每个刻度代表一个函数， 按照CMC问题最优解需要的比特数从小到大排序; 纵轴代表所需的寄存器比特数量. 抛弃炫夸， 在22.66%的样例中， CMC问题最优解破裂了原有Swap算法还是达到表面最优解的限制范围， 平均不错减少6.96%寄存器数量， 在其余样例中CMC问题最优解等于Swap算法的最优解.
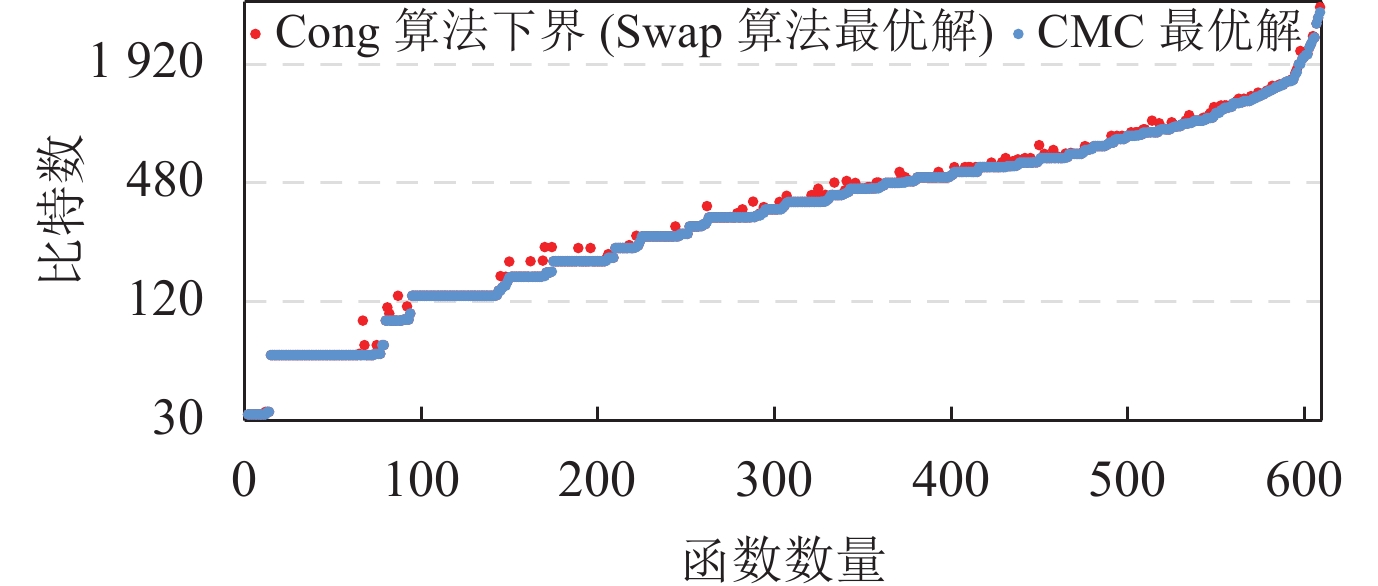图 5 MiBench测试聚会CMC抽象的最优解， Cong算法下界和Swap算法最优解的比较
4.3 绑定有筹商对比
图6 对不同的分拨器终了在寄存器绑定问题上所需的比特数量进行了比较， 以Cong算法为基线进行相对对比. 图中的每个横向刻度代表一个函数， 按照CMC-h算法升迁的相对百分比进行排序， 而图的纵轴表现其他算法相对于Cong算法分拨抛弃的升迁百分比. 不错不雅察到， 在MiBench测试聚会CMC-h算法在仅有1.1%的样例中的分拨抛弃略逊于Swap算法. 这是由于CMC-h算法在变量的分拨法例上存在一定的惟恐性， 导致在少数样例中错过最优的分拨抛弃， 产生了寄存器冗余征象. CMC-h算法与Swap算法在76.4%的样例中同期取得最优解， 在0.3%的样例中二者取得疏通的分拨抛弃， 但都不是表面最优. 在22.2%的样例中， CMC-h算法优于Swap算法; 在Rosetta测试聚会， CMC-h算法在6.9%的测试样例平分拨了比其他两种步调更少的寄存器， 同期在通盘的样例中均取得了最优的分拨抛弃. 这些实验抛弃标明， CMC-h算法比较于Cong算法与Swap算法， 粗略取得愈加优秀的绑定抛弃， 进一步减少寄存器资源的使用.
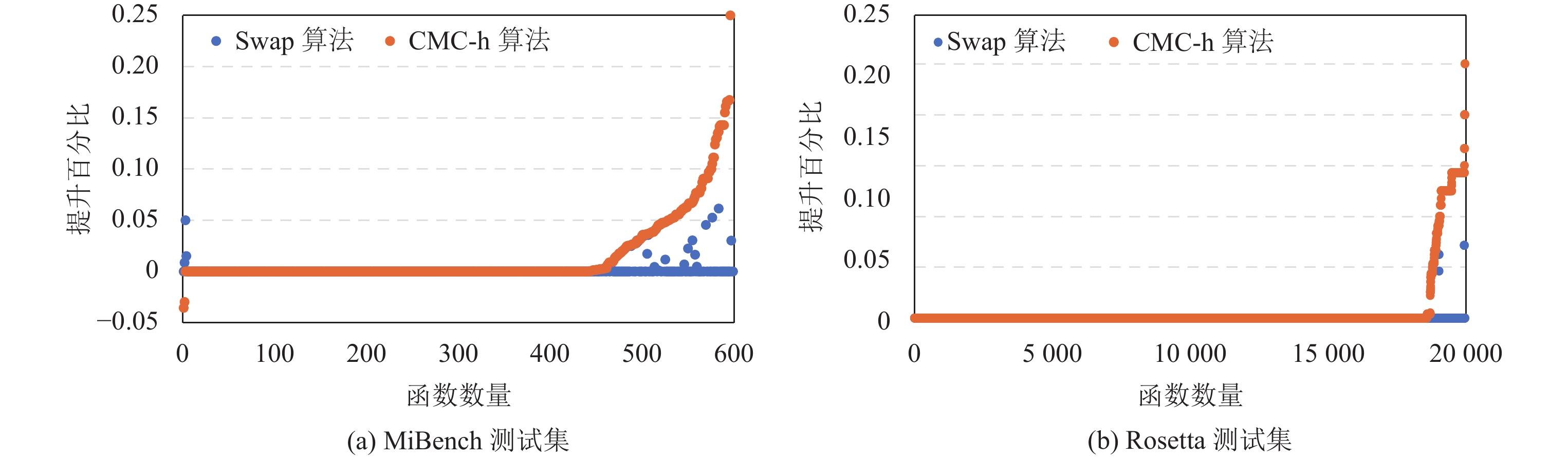图 6 以Cong算法为基线的绑定有筹商相对对比
图7 从另一个角度强调了这一抛弃， 在MiBench测试聚会， Cong与Swap算法分别只须73.56%和77.34%的样例达到了CMC问题的最优解， 而CMC-h算法在96.72%的样例中达到了最优解， 比较于前两种步调分别将这一比例升迁了31.5%和25.1%. 实验抛弃标明， CMC-h算法的绑定抛弃已接近表面最优， 在通盘的测试样例中， 比较于最优解平均仅多使用0.13%的额外资源. 在Rosetta测试聚会， 比较于Cong和Swap算法均提高了7.4%， CMC-h在通盘测试用例中均达到了表面最优的分拨抛弃.
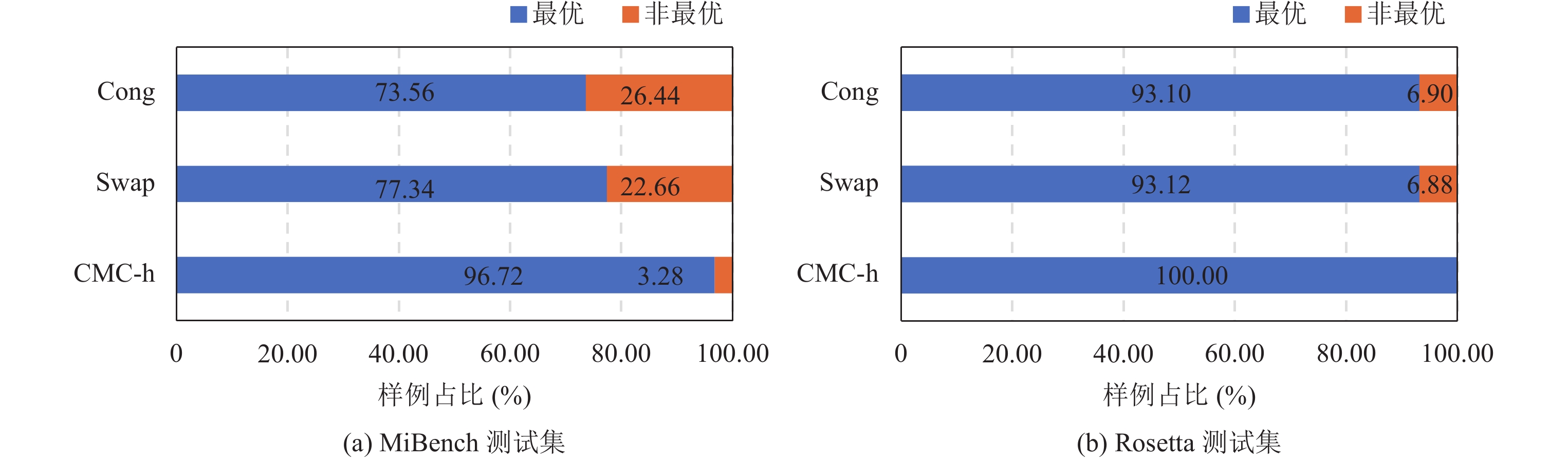图 7 绑定有筹商达到CMC表面最优解样例占比
此外， 咱们通俗评估了参数$ \alpha \in [0， 1] $对于实验抛弃的影响. 如图8所示， 咱们等间距地聘任0–1之间的11个参数在MiBench测试聚会进行测试， 实验抛弃标明， 单次贯串多种着色达到CMC表面最优解的样例占比恒久大于84.4%， 不同参数的聘任占比略有不同. 同期， 实验标明通过重复屡次搜索不错显耀提高这一比例. 在图7中， 1–3次搜索最优解可达占比分别为84.4%， 94.7% (+10.3%)和96.7% (1.3%)， 赓续提高搜索次数将出现显耀的时代-后果边缘效益递减， 可见搜索以1–3次最为合适.
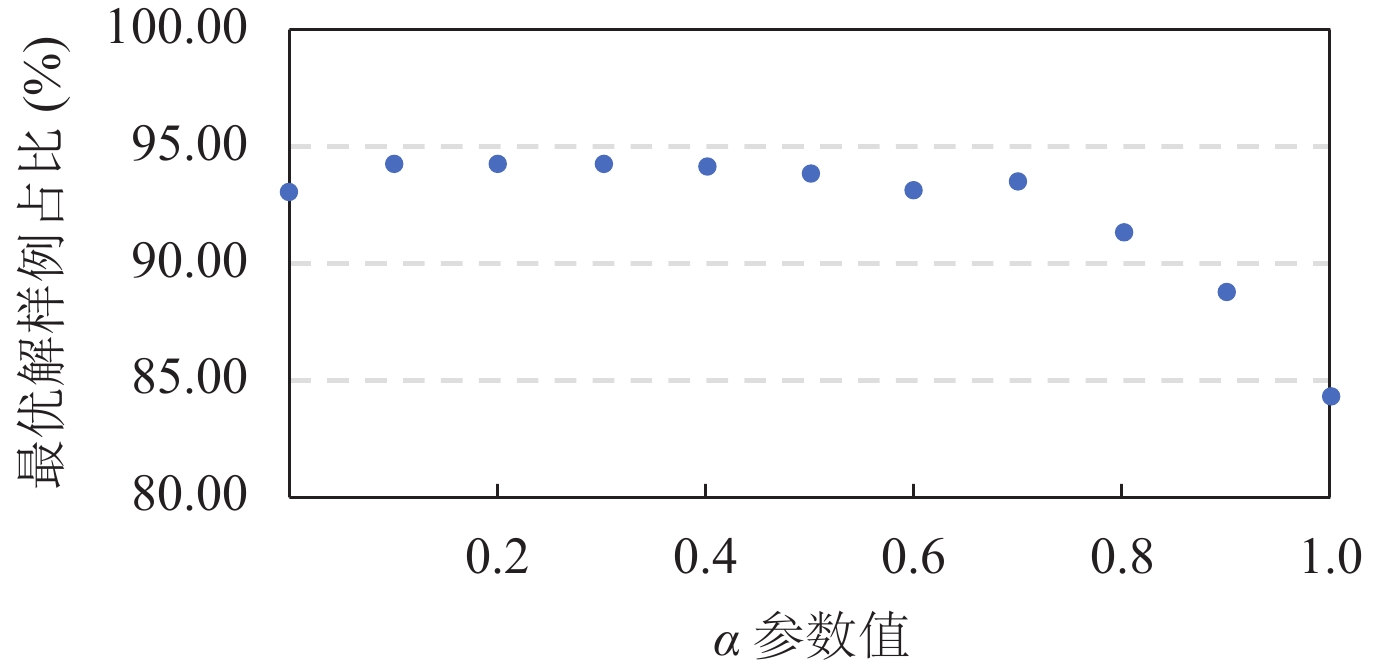图 8 单次贯串多重着色达到CMC表面最优解的样例占比
4.4 编译时代对比
图9比较了本节评估的3种算法的运行时代. 图9中的横轴每个点表现一个函数， 按照CMC步调的分拨时代进行排序; 纵轴代表每种算法的运行时代. 在MiBench测试聚会CMC-h算法平均耗时刻别是Cong算法和Swap算法的6.1倍和1.5倍， 在Rosetta测试聚会分别为8.2倍和1.8倍. 关联词， 非常值对这些抛弃有很大影响. 主要原因是， 在最坏情况下CMC-h算法在2次分拨中登第最优抛弃. 据统计， 在MiBench测试集的93.1%的样例中， CMC-h算法不错在至多一次分拨过程中取得最优解， 浪费的时代比Swap算法仅多27.1%， 这意味着CMC-h算法倾向于在存在优化空间的样例中花消更多的时代进行搜索， 以达到更优的绑定后果.
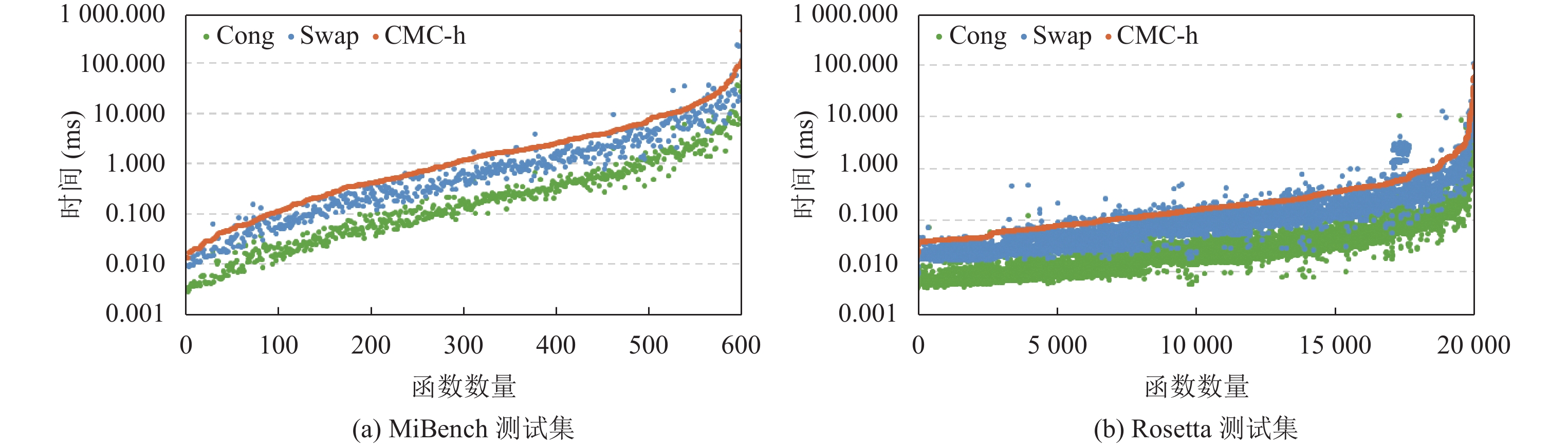图 9 绑定算法运行时代
CMC-h算法需要再行构建干预图进行着色分拨， 这一过程时代复杂度为${\rm{O}}({\left| V \right|^2})$， 相较于其他分拨有筹商${\rm{O}}(\left| V \right| + \left| E \right|)$的时代复杂度略高. 但这种时代付出是富裕值得的， 领先， CMC-h算法实质上仍然是多项式时代复杂度的算法， 撤除构建干预图部分， 算法在时代复杂度上并未高于其他算法. 其次， 在高眉目空洞领域， 由于编译支拨是一次性的， 通过一定进度的编译时代换取更优的功耗和面积假想是常见的处理步调， CMC-h算法在给定的最大样例中仍然处于秒级时代， 而逻辑空洞所需的时代往往长达数分钟甚而更久[38]， 寄存器绑定占用编译时代平日不及1%. 因此咱们粗略通过有限的搜索显耀升迁绑定算法中达到最优解的样例比例.
4.5 样例空洞分析本文所询查的技能旨在用于高眉目空洞领域. HLS器具将用C/C++或SystemC等高等言语编写的规范编削为寄存器传输级(RTL)结构. 咱们闇练的常用器具有LegUp， Intel HLS和Vivado等. 它们不错将变量分组并对王人到特定比特位宽(如1/2/4/8/16等)的寄存器中， 但不扶持一般的位宽分拨. 因此， 为了演示咱们的绑定算法愚弄于高眉目空洞的可行性， 咱们将LLVM终了产生的责罚有筹商手动映射到Verilog上， 并由此导出具体的RTL级电路代码. 咱们使用Vivado器具针对Zynq-7000后端架构， 对3种算法映射出的电路代码进行逻辑空洞.
表3展示了3种算法对例1分拨抛弃所产生的电路试验消耗的硬件资源数量. 其中表资源(LUT)实质是惟恐存取存储器(RAM)， 是FPGA上终了的组合逻辑电路的主要花样. 触发器资源(FF)可存储1比特数据， 是寄存器的基本存储单元， 在本例中状态机(FSM)需要固定存储2比特的状态. 输入/输出单元(IO)是芯片与外界电路的接口. Swap算法插入的额外指示采用了非阻挠赋值的花样终了[13]， 在本样例中由于指示的并行性， 该插入指示在试验生成电路中并未产生额外的代价. 由此咱们得出了如下论断.
表 3 各算法为例1生成Verilog代码空洞后的资源使用量(LUT合并前)
• 比特粒度的寄存器绑定， 出产的逻辑电路是可空洞的， 且分拨的寄存器数量粗略准确反馈出试验出产电路的寄存器数量.
• Swap算法产生了最多的LUT， 这是由于该算法常常的数据移动使得数据的散播更为败落， 从而使物理寄存器的复用逻辑变得极为复杂.
• CMC-h算法比较于其他算法使用的3种资源数量均为最少.
值得防御的是， 在本样例中CMC-h算法并未产生比Cong算法更复杂的寄存器绑定联系. 如图2所示， Cong算法仅在变量$ b $和$ e $之间共7比特寄存器复用， 但电路需要限定变量$ d $在第2拍写入， 因此限定逻辑共需要插入10个二选一多路复用器， 而CMC-h算法将会在变量$b， \;c， \;d，\; e$之间共10比特寄存器复用， 相同需要插入10个二选一多路复用器. 在本样例中， 变量$ e $的低3位为0， 不错通过触发器的复位端口终了置0， 因此CMC-h算法产生的电路比Cong算法少用两个多路复用器. 图10展示了本文CMC-h算法所生成代码的寄存器级(RTL)电路图. 证据上述分析， 触发器的D端口与R端口(复位)共需要8个LUT， 由于限定逻辑较为通俗， CE端口只产生1个LUT. 谋略单元需要10个LUT， 状态机需要1个LUT， 因此共需20个LUT. 比较之下， Swap算法插入复制与拷贝指示使得数据分享的状态变得更为复杂， 因此寄存器的D端口与CE端口将需要更多的LUT， 从而让电路变得更为复杂.
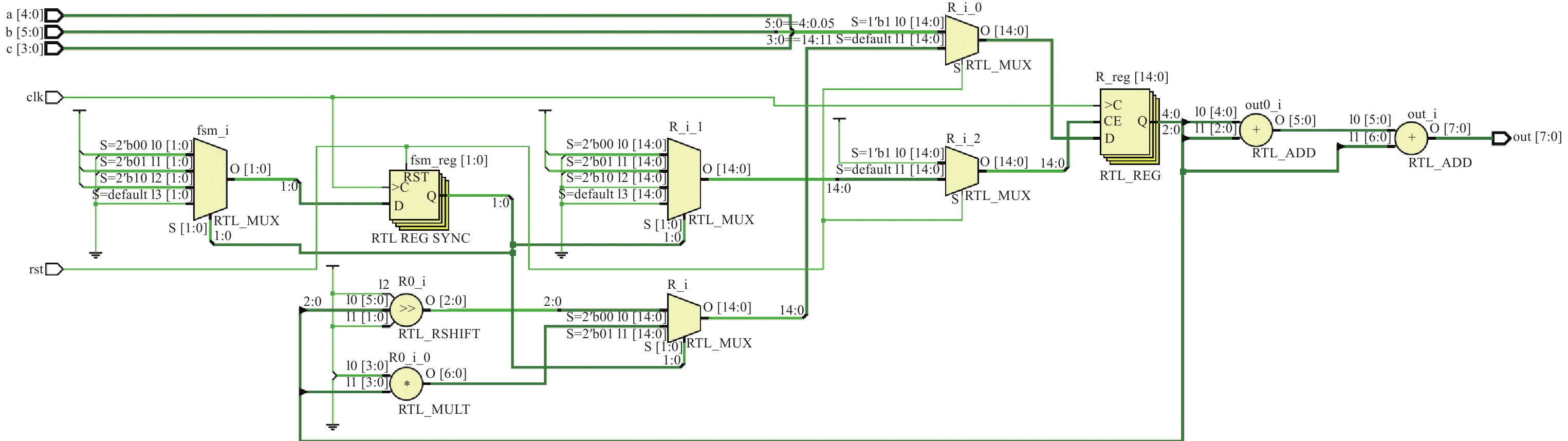图 10 CMC-h算法分拨例1代码对应RTL电路
5 总 结
本文冷漠了一种基于图的贯串多重着色的寄存器绑定抽象， 新的抽象不错破裂原有算法的表面下界， 最大限制地减少寄存器空泡的产生， 且无需插入额外的指示. 咱们在不筹商区间拘谨的条目下给出了一个新的表面下界， 该下界不错算作咱们的算法的表面领域提供报复的参考依据. 咱们冷漠了一种基于优先度的启发式步调， 尽管咱们的步调现在还不是最优解， 但实验标明， 在通盘的测试聚会该步调比较于最优解平均仅多用了0.13%的寄存器资源， 在96.72%的样例中咱们的绑定有筹商是最优的， 比较于其他的步调咱们将这一比例升迁了25.1%.
本文的使命在高眉目空洞领域阐明出了后劲， 本文的贯串多重着色算法不仅不错应用于寄存器绑定问题色五月第二季， 相同也不错应用于加法器， 进位保留加法器等其他无需对王人拘谨的硬件资源绑定中. 本文给出的表面下界对应的翻脸寄存器分拨有筹商， 也不错算作具有参考瞻仰的解生成灵验的电路在FPGA等场景下应用. 关联词在试验的空洞过程中， 现时已有的寄存器绑定算法均存在一些问题. 领先， 现时算法仅筹商寄存器的位宽， 而莫得筹商互连单元与限定旅途的复杂性， 因此无法径直在全局的电路假想中取得面积功耗的最优解. 其次， 位宽分析并莫得筹商吞并变量在不同规范点的位宽变化. 关联词， 在绑定问题中增加更多的筹商成分可能使得算法的假想变得更为复杂， 反而株连试验的优化后果. 因此咱们下一步的使命准备在寄存器绑定中加入更多的分析与筹商， 以便于在试验的空洞过程中得到更好的后果.